The "Polite" Merge Sort
Another old-classic problem: the Merge Sort.
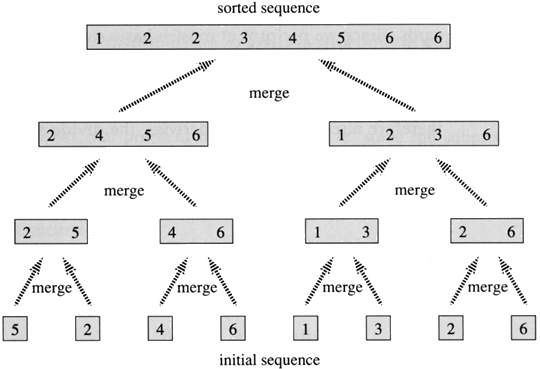Merge Sort Algorithm
The problem of the classical implementation
The whole algorithm is explained in the wikipedia link above, so I’ll focus on the problem here.
The Merge Sort is an in-place-sorting-algorithm that requires some support memory to do it’s calculations. At the “merge step”, an amount of memory as large as the current portion of array being merged is allocated to be used as priority queue (again, the why is easy to find on the web). After this memory is used, normally get’s released.
Theoretically speaking, the amount of memory that at every recursive call get’s created is always <= size-of-input-array. So, no big deal: we knew it.
Unfortunately in practice this is not always a good idea: malloc(...) and free(...) are System Calls, and those are expensive to do. They normally require Context Switches and other system operations that I can’t advice to do without properly thinking through your code.
A more “Polite” Merge Sort
So, because we know the amount of memory that is going to be needed by this algorithm, why don’t we design one that takes it in the beginning and doesn’t bother the Operating System anymore? Good idea!
The thing we need is an array of the same size of the input. Every recursive call of the algorithm, given that it operates on a fixed portion of the input array, will do great operating in the same way on this “support array”.
Not Polite Enough?
A small tweak: when the size input array of the Kth is 2, I avoid to do another recursive call. Instead, I just swap the 2 values if they are not already sorted.
Very “basical” tweak, but, for the sake of it, have fun to calculate how many recursive call I avoid.
…
Done? Yes, if M is the number of recursive calls that this algorithm will normally generate, I avoid M/2 calls. The logical structure of the calls of this problem, as in the example image above, is a Balanced Binary Tree. And in such structure the number of Leaf is equal to M/2, if M are the nodes. Quite a relieve for the call stack, isn’t it! ;)
The code
#include <stdio.h>
#include <stdlib.h>
// === Polite Merge Sort ===
// This implementation of Merge Sort is defined "polite", because it tries
// to bother the Operating Systems as less as possible.
//
// Instead of allocating and freeing memory at every intermediate step
// to implement a the priority queue required to sort do the "MERGE STEP",
// it requires to pass at input an empty support array of the same size
// of the input array.
//
// The support array is going to be the solely memory used as support.
void polite_merge(int* array, const unsigned int l_limit, const unsigned int m_limit, const unsigned int r_limit, int* support_array) {
// Create 3 Peace Marker
unsigned int i; // For the 'array'
unsigned int j; // For the 'left part of the array already ordered'
unsigned int k; // For the 'right part of the array already ordered'
// Copy the portion of sorted arrays in the support array (like a static priority queue)
for ( i = l_limit; i <= r_limit; ++i ) {
support_array[i] = array[i];
}
// Set the Peace Markers
i = j = l_limit; // 'i' and 'j' both start from the Left
k = m_limit + 1; // 'k' starts from the Middle + 1
// Merge the 2 sorted portions
while ( j <= m_limit && k <= r_limit ) {
if ( support_array[j] < support_array[k] )
array[i++] = support_array[j++];
else
array[i++] = support_array[k++];
}
// Add the remaining sorted portions (if any)
while ( j <= m_limit ) array[i++] = support_array[j++];
while ( k <= r_limit ) array[i++] = support_array[k++];
}
void polite_merge_sort(int* array, const unsigned int l_limit, const unsigned int r_limit, int* support_array) {
unsigned int middle;
if ( l_limit == r_limit ) {
// Nothing to do => Only 1 element - already sorted
} else if ( 1 == r_limit - l_limit ) {
// Only 2 elements - swap them if not yet sorted
if ( array[r_limit] < array[l_limit] ) {
// Swap in place - cool!
array[r_limit] ^= array[l_limit];
array[l_limit] ^= array[r_limit];
array[r_limit] ^= array[l_limit];
}
} else {
middle = (l_limit + r_limit) / 2;
polite_merge_sort(array, l_limit, middle, support_array);
polite_merge_sort(array, middle + 1, r_limit, support_array);
polite_merge(array, l_limit, middle, r_limit, support_array);
}
}
This is designed to handle only Integers’ Array, but it can easily adapted to whatever kind of data you mean to sort.